「AtCoder Beginner Contest 144」に参加しました（＆A-E問題解説）

コンテストページはこちら

結果

4完 [A(100), B(200), C(300), E(500)] 46:53 ペナルティ: 0
・順位: 805位 (Rated内?位)
・パフォーマンス: 1446 (水)
・Rating変化: 1427 -> 1429 (+2)

お知らせ

ABC142，143 の解説はお休みとなります。要望があれば，各問題についての解説を書きます。
今回から，一部の問題において， Python での実装例を掲載しています。

各問題の解法

A問題 “Weather Prediction” (100点)

コンテスト中の提出
C++ での提出
Python での提出

20 以下の正整数 \(A, B\) が与えられるので，2 数ともが \(9\) 以下 であるかを判定し， \(9\) 以下ならば \(A \times B\) を計算する問題です。
C++ では，整数の比較は < > <= >= == != などの演算子を使い，判定した結果で分岐するには if 文を使います。”oo と xx どちらも満たす場合” を表すには， && 演算子，2 数の乗算には * 演算子を使います。

計算量 \(O(1)\)

実装例

#include <iostream>

using namespace std;

int main() {
  int A, B;
  cin >> A >> B;
  if (A <= 9 && B <= 9) {
    cout << A * B << endl;
  } else {
    cout << -1 << endl;
  }
}

a, b = map(int, input().split())
print(a * b if a <= 9 and b <= 9 else -1)

B問題 “81” (200点)

コンテスト中の提出
C++ での提出
Python での提出

正整数 \(N\) が与えられるので，\(x \times y\ (1 \leq x, y \leq 9)\) と表せるかを判定する問題です。
2 重 for 文などで判定することができます。詳しくは実装例を参照してください。

計算量 \(O(1)\)

実装例

#include <iostream>

using namespace std;

int main() {
  int N; cin >> N;
  bool ok = false;
  for (int x = 1; x <= 9; x++) {
    for (int y = 1; y <= 9; y++) {
      if (x * y == N) ok = true;
    }
  }
  cout << (ok ? "Yes" : "No") << endl;
}

n = int(input())
print("Yes" if n in [i * j for i in range(1, 10) for j in range(1, 10)] else "No")

C問題 “Walk on Multiplication Table” (300点)

コンテスト中の提出
C++ での提出
Python での提出

\(10^{12}\) 以下の 正整数 \(N\) が与えられます。
この整数を \(i \times j\ (i, j \in \mathbb{N})\) と表したとき，\(i+j-2\) の最小値を求める問題です。
まず，愚直に考えると [1, N] の範囲で 2 重ループを回し，\(ij = N\) となる 2 整数の和の最小値を更新すればよいです。しかし，これは \(O(N^2)\) となり，到底間に合いません。
ここで，約数 (つまり，\(ij = N,\ i \leq j\) となる \(i, j\) すべて) を列挙する際，一方の約数 \(i\) は \(\sqrt N\) 以下であることを利用します。もう一方の約数 \(j\) は \(N \div i\) から求まるので，すべての約数は \(O(\sqrt N)\) で求まることがわかります。
あとは，すべての \(i,j\) の組を列挙し，\(i+j-2\) の最小値を求めれば良いです。\(1 \times N = N\) であることは自明なので，\(1 + N – 2 = N – 1\) を初期値にしておきましょう。

計算量 \(O(\sqrt N)\)

実装例

#include <iostream>
 
using namespace std;
 
int main() {
  long long N;
  cin >> N;
  long long ans = N - 1;
  for (long long i = 1; i * i <= N; i++) {
    // N / i にあまりが発生したら i は N の約数ではない
    if (N % i) continue;
    long long j = N / i;
    ans = min(ans, i + j - 2);
  }
  cout << ans << endl;
}

import math

n = int(input())
print(min([i + (n // i) - 2 for i in range(1, int(math.sqrt(n)) + 1) if n % i == 0]))

D問題 “Water Bottle” (400点)

C++ での提出
Python での提出

底面の各辺が \(a\ cm\) の正方形で，高さが \(b\ cm\) の直方体を \(d^\circ\) 傾けたとき，水が最大で \(x\ cm^3\) 入る。このときの \(d\) を求める問題です。
まず，傾ける角度と入る水の体積には連続性があります。すなわち， \(S>T\) のとき， \(S^{\circ}\) 傾けた場合と \(T^{\circ}\) 傾けた場合では，後者のほうが入る水の体積は多いということです。
よって， \(d^\circ\) 傾けたときに入る水の量を計算する関数 \(f(d)\) を書いて，\(x\ cm^3\) の水が入るかどうかでこの \(d\) を二分探索すればよいです。
さて，この \(f(d)\) を書くのが問題です。この計算式は「\(d\) 度傾けたときに入る容量が \(\frac{a^2b}{2}\) を超えているかどうか」で分ける必要があります。どちらの場合でも，面積の問題と見ることができ，奥行き \(a\) をかけることで体積に変換することができます。

\(d^\circ\) を弧度法 (ラジアン) で表した角度 \(d \cdot \frac{\pi}{180}\) を \(\theta\)
\(\theta\) 傾けたときに入る容量 を \(A\)
最大の容量 \(a^2b\) を \(B\) とします。

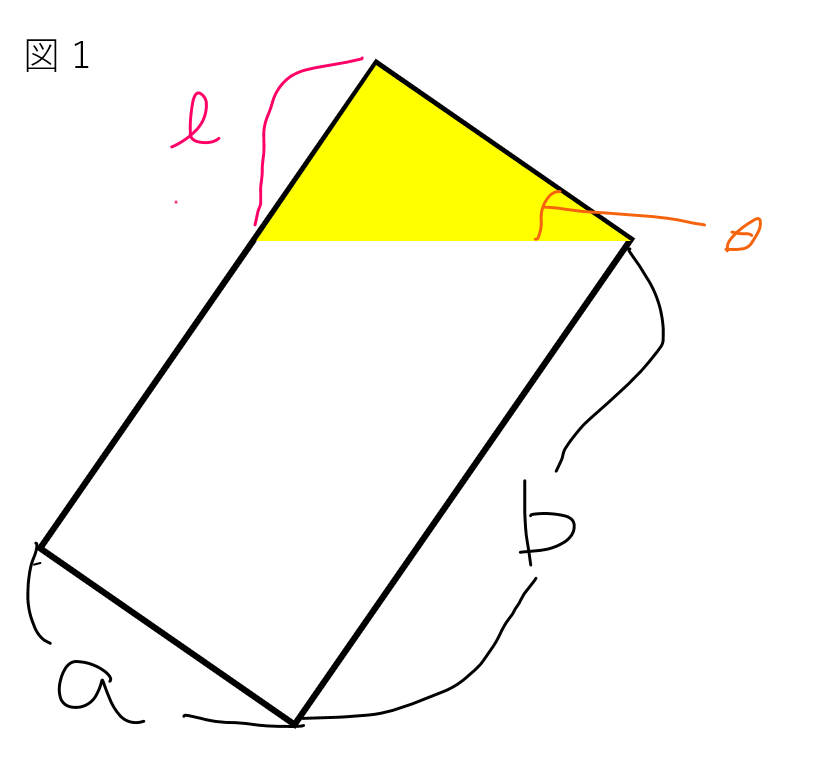
\(\frac{B}{2} \leq A\) の場合 (図 1)

\(\frac{B}{2} \leq A\) の判定はこのあと説明します。
一度面積の問題とします。ここで，長方形全体の面積 \(\frac{A}{a}\) を \(A’\) とおきます。
ここで，入る面積は， \(A’\) から黄色の三角形の面積を引くことにより求まります。この三角形の面積を求めるには，線分 \(l\) の長さ を求める必要があります。この長さは，\(\tan\theta = \frac{l}{a}\) より， \(a\cdot\tan\theta\) となります。
また，先ほどの \(\frac{B}{2} \leq A\) は， \(l \leq b\) であるかで判定することができます。
以上より，黄色の三角形の面積は
\[\frac{a^2\tan\theta}{2}\]
となり，この状態での入る水の体積は，[全体の長方形の面積 – 黄色の三角形の面積] \(\times a\) つまり
\[a \cdot (ab – \frac{a^2 \cdot \tan\theta}{2}) = a^2b – \frac{a^3\tan\theta}{2}\]
となります。

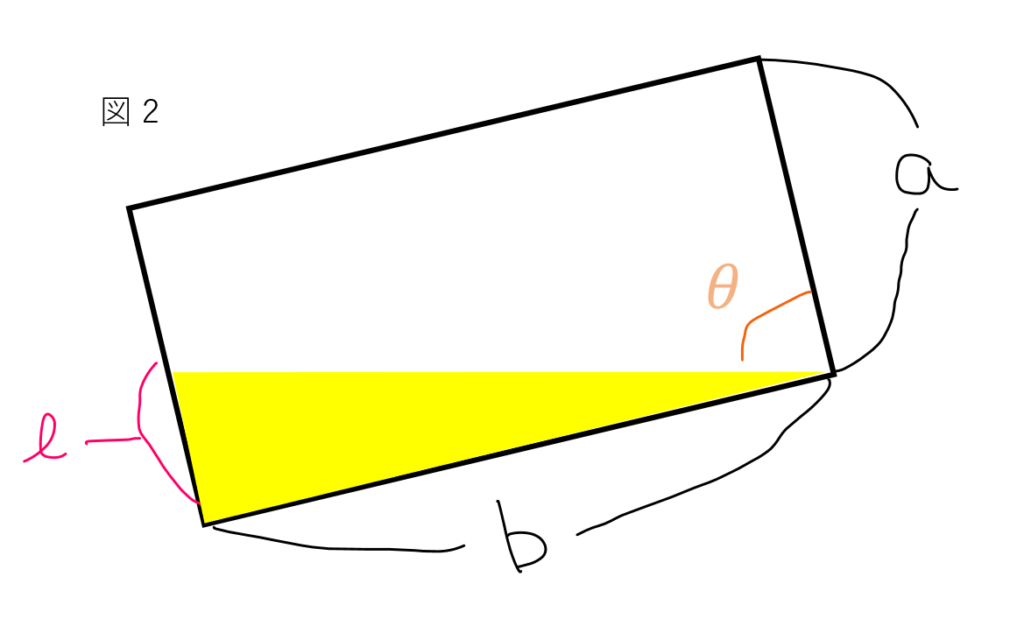
そうでない場合 (図 2)

ここでも，一度面積の問題とします。
今回は，入る面積を黄色の三角形とし，底辺を \(l\) とします。
長方形の底辺の一部である \(l\) の長さは，以下の計算式で求めることができます。
\[
\begin{eqnarray}
\tan(90^\circ – \theta) &=& \frac{l}{b} \\ &=& \frac{1}{\tan\theta} \\
\Leftrightarrow \frac{lb}{b} &=& \frac{b}{\tan\theta} \\
\Leftrightarrow l &=& \frac{b}{\tan\theta}
\end{eqnarray}
\]
これにより求まった三角形の面積 \(\frac{lb}{2} = \frac{b^2}{2\tan\theta}\) に \(a\) をかけた \(\frac{ab^2}{2\tan\theta}\) がこの状態で入る水の体積となります。

あとは，求まった角度 \(d\) が答えとなります。
以上の式を利用して実装します。

計算量 \(O(1)\)

実装例

#include <iostream>
#include <cmath>
#include <iomanip>

using namespace std;

int a, b;

double f(double d) {
  double theta = d * M_PI / 180;
  if (a * tan(theta) <= b) {
    return a * a * b - a * a * a * tan(theta) / 2;
  } else {
    return a * b * b / (2 * tan(theta));
  }
}


int main() {
  int x;
  cin >> a >> b >> x;

  double ok = 0;
  double ng = 90;

  for (int count = 0; count < 100000; count++) {
    double mid = (ok + ng) / 2;

    if(f(mid) <= x) ng = mid;
    else ok = mid;
  }
  cout << fixed << setprecision(7) << ok << endl;
}

Python での実装例は上記「Python での提出」をご覧ください。

E問題 “Gluttony” (500点)

コンテスト中の提出
C++ での提出

長さ \(N\) の数列 \(A, K\) が与えられるので，「この 2 つの数列を並び替える」「\(A_i\) が非負数となる範囲で，数値を合計で \(K\) 減らす」の操作を適切に行い，\(max(A_i\cdot F_i)\) を最小化する問題です。
まずは (\(A_i\) が調節できない場合) \(F_i\) が大きいものには \(A_i\) が小さいものを割り当てたいと考えるはずです。そのため，\(F\) を降順に，\(A\) を昇順にソートします。
また，「成績を \(x\) 以下にできるか」という条件で二分探索をすることにより，この値を決め打つことができます。
「成績を \(x\) 以下にできるか」は，「各 \(i\) について， \(x > A_i\cdot F_i\) の間 \(A_i\) を減らし，減らした数の合計が \(K\) 以下であるか」と言い換えることができます。
この “減らした数の合計” は以下の数式と同値です。
\[
\sum^{N-1}_{i=0} \mathrm{max}\left(0, \left\lceil\frac{A_i \cdot F_i – x}{F_i}\right\rceil\right)
\]
以上を実装します。

計算量 \(O(N\ \mathrm{log} (\mathrm{max}(A_i) \cdot \mathrm{max}(F_i)))\)

実装例

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int main() {
  int N;
  long long K;
  cin >> N >> K;
  vector<int> A(N), F(N);
  for (int i = 0; i < N; i++) cin >> A[i];
  for (int i = 0; i < N; i++) cin >> F[i];

  sort(A.begin(), A.end());
  sort(F.rbegin(), F.rend());

  long long ng = 0, ok = 1000000000001;
  while(ng < ok) {
    auto mid = (ng + ok) / 2, sum = 0LL;
    for (int i = 0; i < N; i++) {
      sum += max(0LL, ((long long)A[i] * F[i] - mid + F[i] - 1) / F[i]);
    }
    if (sum <= K) ok = mid;
    else ng = mid + 1;
  }
  cout << ok << endl;
}

(Python での実装・提出は省略しています。)

全体の感想

今回は D 問題で三角比が出てこなくて解けなかったので，残念な結果となりました。（これでもレートが微増するのはびっくりですが）
「全国統一プログラミング王決定戦 予選」や「JOI 2019 / 2020 二次予選」に備えてしっかりと精進していきたいと思います。
D 問題の解説を書くの，めちゃめちゃ疲れました…(D だけで 3 時間くらいかかった)